This document briefly describes the features of the spatial discretizations available in MPI-AMRVAC. The different options can be set in the methodlist of the input par file. For a more extensive description, you can read the article Comparison of some FCT and TVD Schemes. Also, the paper using MPI-AMRVAC has info on the various methods, see 'Parallel, grid- adaptive approaches for relativistic hydro and magnetohydrodynamics', R. Keppens, Z. Meliani, A.J. van Marle, P. Delmont, A. Vlasis, & B. van der Holst, 2011, JCP. doi:10.1016/j.jcp.2011.01.020. A more recent update is 'MPI-AMRVAC FOR SOLAR AND ASTROPHYSICS', O. Porth, C. Xia, T. Hendrix, S. P. Moschou and R. Keppens ApJS. doi:10.1088/0067-0049/214/1/4.
The acronyms TVD, TVDLF, and TVD-MUSCL stand for Total Variation Diminishing, TVD Lax-Friedrich, and TVD Monotonic Upwind Scheme for Conservation Laws, respectively. Then, depending on the physics module selected, you also have HLL, HLLC, and HLLD schemes, which are due to harten Lax, van Leer, with the HLLC variant including a treatment for the Contact discontinuity, as e.g. described for Euler gas dynamics in E.F. Toro, Riemann solvers and numerical methods for fluid dynamics (Berlin, Springer-Verlag, 1997), and with the HLLD variant for MHD including multiple discontinuities, which was invented by Miyoshi and Kusano in Journal of Computational Physics, 208, 315-344 (2005).
Not all methods are available or meaningfull for all physics modules. In fact, we have the following combinations typically:
Physics Schemes -------------------------------------------------------------------------- rho TVDLF, HLL, HLLC, TVD (Roe solver), TVDMU (Roe solver), FD HD TVDLF, HLL, HLLC, TVD (Roe solver), TVDMU (Roe solver), FD MHD TVDLF, HLL, HLLD, TVD (Roe solver), TVDMU (Roe solver), FD
Also, the method can be selected per AMR grid level, but one can not combine different stepsize methods (hence, TVD is the only second order onestep method, while all others can be used with all steps time stepper/integrator setting). In MPI-AMRVAC, the flux_scheme is thus an array of strings, one string per level up to nlevelshi. Some more info follows on the various methods.
HLL HLLC and HLLD schemes
The TVDLF scheme hence uses minimal info on the wave speeds, and in combination with AMR and its inherent robustness due to its diffusive nature, it is readily usable for any system of conservation laws at minimal implementation costs. But TVDLF maybe too diffusive to resolve details in your applications. Maximal wave speed info is used in a full Roe-type approximate Riemann solver as employed by TVD or TVD-MUSCL, where all characteristic wave speeds (7 in total for (relativistic) MHD) as well as the wave strengths are deduced from the eigenvalues, as well as right and left eigenvector pairs of the flux Jacobian. However, TVD or TVD-MUSCL is limited to second-order accuracy and not the most efficient one. The simpler HLL, HLLC, and HLLD solvers, make further approximations to their corresponding representation of the Riemann fan, as schematically illustrated below. 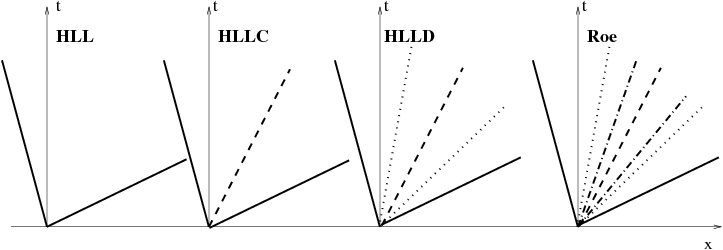
In these approximate Riemann solvers, the HLL is available for all physics modules but the most diffusive one. The HLLC is designed for HD physics and gives unreliable results for MHD. The HLLD works only for MHD and gives the best resolution with higher efficiency than Roe solver.
TVDLF Scheme
The TVD Lax-Friedrich method is robust, in most cases there are no spurious oscillations, but it is somewhat more diffusive than HLL, HLLC, HLLD or TVD methods. Since it does not use a Riemann solver, it is the fastest. The Courant number should be less than 1, courantpar=0.8 is recommended. Second order time discretization is best achieved by a Hancock predictor step, so the corresponding typepred1='hancock'. TVDLF can be used with dimsplit=F, it is also preferred for steady state calculations. The second order TVDLF scheme flux_scheme='tvdlf' uses limiters. There are many choices available: the 'minmod' limiter gives the smoothest result, the 'woodward' limiter is sharper, and the 'superbee' limiter is probably too sharp. The **'woodward'** limiter is recommended, but note that the default is the most robust limiter='minmod'. The various options can be found in the mod_finite_volume.t module, in the subroutine dwlimiter2. The slope limiting is performed on the primitive variables. You can even employ limiting on logarithmically stretched variables (which should be positive, like a density or pressure), by setting the loglimit flags. You can also use third order accurate limiter='ppm', but the code will run with a wider ghost cell region, namely nghostcells=4. A third order limiter **'cada3'** (also known as LIMO3) only needs nghostcells=2 ghost cell layers .
TVD-MUSCL Scheme
The TVD-MUSCL scheme flux_scheme='tvdmu' is a two-step TVD algorithm using the same Hancock predictor step and upwinding as TVDLF, and a characteristic based Riemann solver similar to the TVD method. At the moment Riemann solvers are implemented for adiabatic hydrodynamics, hydrodynamics, and full MHD. The scalar transport equation has a trivial Riemann solver. The scheme has comparable resolution to the non-MUSCL TVD method. The Courant number should be less than 1, courantpar=0.8 is recommended. TVD-MUSCL can be dimensionally split dimsplit=T or unsplit dimsplit=F. The multistep Runge-Kutta schemes can be applied, such as time_stepper='fourstep' with time_integrator='rk4'. Linear Riemann solvers can produce non-physical solutions. This can be eliminated by the use of an entropy fix, controlled by typeentropy and the entropycoef. The default is typeentropy='nul'. See the details for the entropy fixes in the respective mod_PHYS_roe.t files, as well as in the mod_tvd.t module.
TVD Scheme
The non-MUSCL TVD method flux_scheme='tvd' with Roe approximate Riemann solver is one of the most accurate and efficient of the implemented schemes. There are a few variants of the TVD scheme, but the default is typetvd='roe'. Details are in the mod_tvd.t module. This solver has to be dimensionally split, set dimsplit=T. The Courant number should be less than 1, courantpar=0.8 is recommended. The same limiters can be used as for TVDLF and TVD MUSCL, but they are applied to the characteristic waves, rather than to the primitive variables. The order of the characteristic waves is defined in the mod_PHYS_roe.t files. The **'woodward'** limiter is recommended, but note that the default is **'minmod'**. The entropy fix for the Riemann solver is given by the typeentropy array, it has the same meaning as for the TVD-MUSCL method, and for MHD, the divergence B problem should also be taken care of.
2nd Order Central Difference Scheme
The explicit central differencing schemes are not stable by themselves for advection dominated problems. The second order central difference scheme ('cd') is used by the TVD scheme before the limiting is applied. Otherwise it is useful for testing a few time steps, since this scheme contains no artificial fluxes, thus comparison with analytic formulae is straightforward. It is straightforward to generalize this central difference approach to higher order accuracy, at the expense of introducing a wider stencil.
High order finite difference FD Scheme
This scheme flux_scheme='fd' implements conservative finite differences with global Lax-Friedrich flux splitting. It can be used with almost all limiters (exluding ppm) and yields high order accuracy in space. For second, third and fifth order reconstruction you can set e.g.: limiter='koren'/'cada3'/'mp5'.
Maintaining the div B=0 Condition
In multidimensional MHD the numerical conservation of divergence of magnetic field div B is not guaranteed by the standard TVD or HLL type schemes. This can lead to inaccuracies as well as instablilities. For all the schemes below, you can influence how to compute div B, by setting typegrad and typediv, along with gradient_limiter. This allows to select either a standard central difference evaluation, or one evaluated after the cell-center values have been reconstructed to the cell edges. User can select one of the following methods by select typedivbfix and related parameters in mhd_list of par file.
constrained transport fix: typedivbfix='ct'
The upwind constrained transport (CT) method by Gardiner and Stone in Journal of Computational Physics, 205, 509-539 (2005), type_ct='uct_contact' (default), or by Del Zanna, L., Zanotti, O., Bucciantini, N., & Londrillo, P. in Astronomy & Astrophysics , 473, 11 (2007) type_ct='uct_hll', using staggered grid for magnetic field, can preserve initial div B to round off errors. A simple non-upwinding version of ct is through averaging electric fields from neighbors type_ct='average'. It only works with HLL and HLLD Riemann flux schemes in the current implementation. It works in Cartesian and non-Cartesian coordinates with or without grid stretching. It works with finite non-zero resistivity. Initial conditions and boundary conditions for magnetic field have to be given at corresponding cell faces instead, or vector potential is given at corresponding cell edges, see examples: tests/mhd/solar_atmosphere_2.5D. Note that when using AMR, the div B preserving prolongation for CT requires even number of ghost cell layers and odd number of ghost layers for some slope limiters, e.g. mp5, is added by one to become even.
Powell fix: typedivbfix='powel'
For multidimensional MHD calculations the non-conservative form of the MHDequations" seems to produce better results than the usual conservative form. The idea is to include source terms proportional to div B into the momentum, energy and induction equations and to add a divergence wave for the Riemann solver. Powell scheme is fast, it stabilizes the Riemann solver, and improves results for TVDLF and similar type methods, but it is non-conservative, and div B is not kept close to zero.
Janhunen fix: typedivbfix='janhunen'
Source term in Powell fix is only added to the induction equation. This approach is usable for both classical and relativistic MHD.
Diffusive fix: typedivbfix='linde'
You can also use the diffusive (parabolic) approach, see the equations. It uses a C_d coefficient quantified by divbdiff, which can be up to 2. This method is by default inactive, identified by divbdiff=1, but it is recommended for many multi-D MHD applications.
Dedner fix: typedivbfix='glm'
This implements the mixed hyperbolic propagating and parabolic dampening of divB using an additional scalar variable psi. The algorithm of 'glm' is described by Dedner et al. as Equation (24) in Journal of Computational Physics 175, 645-673 (2002) doi:10.1006/jcph.2001.6961.
projection fix: typedivbfix='multigrid'
Projection scheme using multigrid Poisson solver by Teunissen and Keppens in Computer Physics Communications 245, 1068, (2019) can be use to remove div B part of B.
Combined fix: typedivbfix='lindejanhunen' or 'lindepowel'
Combining diffusive fix and Janhunen or Powell fix by add both source terms of these methods at the same time.