Program to extrapolate linear force-free fields in 3D Cartesian coordinates, based on exact Green function method (Chiu & Hilton 1977 ApJ 212,873). More...
Functions/Subroutines | |
| subroutine | init_b_fff_data (magnetogramname, qlunit, qbunit) |
| subroutine | calc_lin_fff (ixil, ixol, bf, x, alpha, zshift, idir) |
| subroutine | get_potential_field_potential (ixil, ixol, potential, x, zshift) |
| subroutine | get_potential_field_potential_sphere (ixil, x, potential, nth, nph, magnetogram, theta, phi, r_sphere) |
| subroutine | potential_field_energy_mg (benergy) |
| get potential magnetic field energy given normal B on all boundaries | |
| subroutine | get_potential_field_potential_mg () |
| Solve Poisson equation of scalar potential using multigrid solver. | |
| subroutine | multigrid_bc (box, nc, iv, nb, bc_type, bc) |
| To set boundary condition on physical boundaries for mg Poisson solver. | |
Variables | |
| double precision, save | bzmax |
| double precision, save | darea |
| double precision, dimension(:,:), allocatable, save | bz0 |
| double precision, dimension(:), allocatable, save | xa1 |
| double precision, dimension(:), allocatable, save | xa2 |
| integer, save | nx1 |
| integer, save | nx2 |
Detailed Description
Program to extrapolate linear force-free fields in 3D Cartesian coordinates, based on exact Green function method (Chiu & Hilton 1977 ApJ 212,873).
Usage: 1 In the subroutine usr_set_parameters of mod_usr.t: To extrapolate a linear force free field from a observed magnetogram prepared in a data file, e.g., 'hmiM720sxxxx.dat' replace call init_bc_fff_data('hmiM720sxxxx.dat',unit_length,unit_magneticfield) 'hmiM720sxxxx.dat' must be a binary file containing nx1,nx2,xc1,xc2,dxm1, dxm2, Bz0(nx1,nx2). Integers nx1 and nx2 give the resolution of the uniform-grid magentogram. Others are double-precision floats. xc1 and xc2 are coordinates of the central point of the magnetogram. dxm1 and dxm2 are the cell sizes for each direction, Bz0 is the vertical conponent of magetic field on the solar surface from observations. 2 In the subroutine usr_init_one_grid of mod_usr.t, add lines like:
double precision :: Bf(ixG^S,1:ndir), alpha, zshift
alpha=0.d0 ! potential field !alpha=0.08d0 ! non-potential linear force-free field zshift=0.05d0 ! lift your box zshift heigher to the bottom magnetogram call calc_lin_fff(ixG^L,ix^L,Bf,x,alpha,zshift)
3 Notice that the resolution of input magnetogram must be better than the best resolution of your AMR grid to have a good behavior close to the bottom layer
Function/Subroutine Documentation
◆ calc_lin_fff()
| subroutine mod_lfff::calc_lin_fff | ( | integer, intent(in) | ixi, |
| integer, intent(in) | l, | ||
| integer, intent(in) | ixo, | ||
| l, | |||
| double precision, dimension(ixi^s,1:ndir), intent(inout) | bf, | ||
| double precision, dimension(ixi^s,1:ndim), intent(in) | x, | ||
| double precision, intent(in) | alpha, | ||
| double precision, intent(in) | zshift, | ||
| integer, intent(in), optional | idir | ||
| ) |
Definition at line 101 of file mod_lfff.t.
◆ get_potential_field_potential()
| subroutine mod_lfff::get_potential_field_potential | ( | integer, intent(in) | ixi, |
| integer, intent(in) | l, | ||
| integer, intent(in) | ixo, | ||
| l, | |||
| double precision, dimension(ixi^s), intent(inout) | potential, | ||
| double precision, dimension(ixi^s,1:ndim), intent(in) | x, | ||
| double precision, intent(in) | zshift | ||
| ) |
Definition at line 169 of file mod_lfff.t.
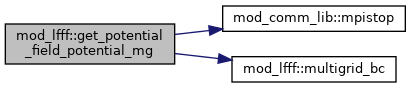
◆ get_potential_field_potential_mg()
| subroutine mod_lfff::get_potential_field_potential_mg |
Solve Poisson equation of scalar potential using multigrid solver.
Definition at line 285 of file mod_lfff.t.
◆ get_potential_field_potential_sphere()
| subroutine mod_lfff::get_potential_field_potential_sphere | ( | integer, intent(in) | ixi, |
| integer, intent(in) | l, | ||
| real*8, dimension(ixi^s,1:ndim), intent(in) | x, | ||
| real*8, dimension(ixi^s), intent(out) | potential, | ||
| integer, intent(in) | nth, | ||
| integer, intent(in) | nph, | ||
| real*8, dimension(nth,nph), intent(in) | magnetogram, | ||
| real*8, dimension(nth), intent(in) | theta, | ||
| real*8, dimension(nph), intent(in) | phi, | ||
| real*8, intent(in) | r_sphere | ||
| ) |
Definition at line 204 of file mod_lfff.t.
◆ init_b_fff_data()
| subroutine mod_lfff::init_b_fff_data | ( | character(len=*), intent(in) | magnetogramname, |
| double precision, intent(in) | qlunit, | ||
| double precision, intent(in) | qbunit | ||
| ) |
◆ multigrid_bc()
| subroutine mod_lfff::multigrid_bc | ( | type(mg_box_t), intent(in) | box, |
| integer, intent(in) | nc, | ||
| integer, intent(in) | iv, | ||
| integer, intent(in) | nb, | ||
| integer, intent(out) | bc_type, | ||
| double precision, dimension(nc, nc), intent(out) | bc | ||
| ) |
To set boundary condition on physical boundaries for mg Poisson solver.
- Parameters
-
[in] iv Index of variable [in] nb number of boundary from 1 to 6 for 3D [out] bc_type Type of b.c.
Definition at line 315 of file mod_lfff.t.
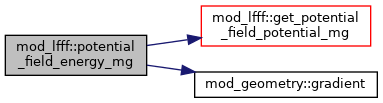
◆ potential_field_energy_mg()
| subroutine mod_lfff::potential_field_energy_mg | ( | real*8, intent(out) | benergy | ) |
get potential magnetic field energy given normal B on all boundaries
Definition at line 248 of file mod_lfff.t.
Variable Documentation
◆ bz0
| double precision, dimension(:,:), allocatable, save mod_lfff::bz0 |
Definition at line 31 of file mod_lfff.t.
◆ bzmax
| double precision, save mod_lfff::bzmax |
Definition at line 30 of file mod_lfff.t.
◆ darea
| double precision, save mod_lfff::darea |
Definition at line 30 of file mod_lfff.t.
◆ nx1
| integer, save mod_lfff::nx1 |
Definition at line 33 of file mod_lfff.t.
◆ nx2
| integer, save mod_lfff::nx2 |
Definition at line 33 of file mod_lfff.t.
◆ xa1
| double precision, dimension(:), allocatable, save mod_lfff::xa1 |
Definition at line 32 of file mod_lfff.t.
◆ xa2
| double precision, dimension(:), allocatable, save mod_lfff::xa2 |
Definition at line 32 of file mod_lfff.t.
